B+ trees

/*

This article is from 

1 youtube ( https://www.youtube.com/watch?v=aZjYr87r1b8 )

2 wikipedia

3 geeks for geeks

4 introduction to algorihtm

5 bunch of website, blog

6 Rosetta code

*/

B+ trees

 B+ trees 는 balanced n - ary search Tree 의 일종이다. n - ary Tree는 말 그대로 한 노드가 자신의 자식노드를 최대 n 개 까지 가질 수 있는 트리이다. 이 때, Search Tree 이므로 각 노드들의 자식 - 부모 관계는 그 노드의 키에 의해 결정된다. Binary Search Tree 가 최대 2개의 자식을 가지는 Bin - ary 이며 임의의 노드가 자신의 key에 의해 양 방향으로 나뉘는 서브트리를 가지는 것을 기억해보자. 

 

 자, 만약 여러분이 Binary Search Tree에 대해 잘 이해하고 있었다면 n-ary search tree 또한 금방 익숙해 질것이다. n - ary search Tree는 자신의 자식 서브트리를 최대 n 개 가질 수 있으며, 그 서브트리를 나누는 key set 을 가진다. 이때 그 key의 set크기는  최대 n-1 개일 수 있다. binary 는 노드의 key를 2-1, 즉 1개 가진다는 것을 기억하자.

자 그렇다면 n-ary search tree는 다음과 같이 생길 수 있다.

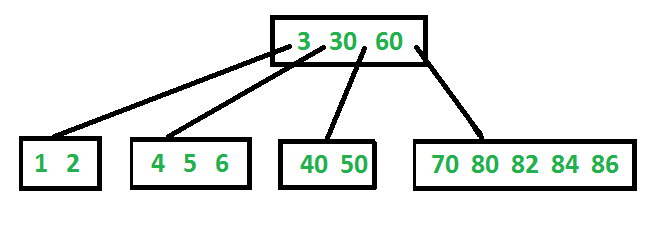
B- tree picture from geeks for geeks
https://www.geeksforgeeks.org/b-tree-set-1-introduction-2/

위 사진은 B- tree이다. 위 그림은 최소 n을 6이상 가지는 n-ary tree의 일종 이라고 볼 수 있다. 

자, B- tree와 B+ tree는 이름이 비슷한 것에서부터 유사하다고 유추할 수 있다. 실제로 B+ tree는 B- tree를 보완하기 위해 나왔고, 몇몇 연산에서 더 나은 수행복잡도를 보인다. 하지만 지금이 포스트는 B+ tree의 implementation 에 대해 이야기 할 것이다. 따라서, 일반적인 B tree 가 가지는 특성을 설명하고 그다음 바로 B+ tree의 implementation에 대해 이야기할 것이다. 

하나는 장담하는데, B- tree를 모른다고 뒤로 가기를 누르지마라. 왜냐하면 급하게 B+ tree를 배우려고 왔는데 B- tree의 진보된 형태라고? 하면서 B- tree를 학습하러 가는것은 그다지 효율적인 일이 아닐것같다. 왜냐하면 이론적인 수행복잡도라던가 B- tree 구현법 이런 것들은 디테일한 부분은 다를지 몰라도 대부분의 맥락은 같으면서 논리가 진행되기 때문이다. 내 생각엔 B+ tree를 배우고 B- tree를 살펴보아도 크게 문제는 없을 것 같다. (어디까지나 내생각)

B tree의 특징

B tree의 가장 큰 특징은

1 n- ary tree 이라는 점이다. 

그리고, 

2 한 노드는 최대 n-1 key 를 가질 수 있다는점( 여전히 이해가 가지 않는다면 Binary search tree에서 임의의 노드는 2 서브트리를 가지며, key가 한개를 가진다고 생각해라. 그리고 그것을 n개로 확장해보자.)

그리고,

3 balanced 하다는 점이다. 이 포스트를 읽으시는 분들은 대개 Balanced Search Tree의 일종인 Red Black tree나 AVL tree에 대해 익숙할 것이다. 사실 복잡도는 Big - O notation에 의해 둘 다 O (lg n) 일것이다. binary 는 로그의 밑이 2이고, m- ary는 로그의 밑이 m일것이다. 즉  lg(2) n  vs lg(m) n 일것인데, Big O notation에 의해 O ( lg n ) 으로 통일된다. 무엇이 더 낫냐 에 대한 질문이 잇을 수 있는데, disc 에서의 연산은 B tree가 더 효율적이라고 한다. 따라서 B tree에 대해 논의 할 때는 Database와 연관되어 많이 서술되는 것 같다. database엔 일반적인 컴퓨터가 셈을 하기에 무리가 있는 엄청난 수의 데이터들이 disc에 쓰여지며 그것을 효율적으로 관리하기 위한 특별한 자료구조가 필요하고, 그 자료구조엔 B tree가 있기 때문이라고 생각한다.

4 Balanced 한 것을 유지하는 것은 모든 leaf node 들이 같은 높이를 이루는 특성에 의해 결정된다. 왜 모든 leaf node들이 같은 높이를 유지하는 지에 대해서는 다음 링크를 참조하라. ( https://youtu.be/aZjYr87r1b8?t=951 ) 사실상 00:00 ~ 18:20 까지 B tree에 대한 큰 특징들을 서술하고 있고, 기존 data들을 indexed 한 것들이라 leaf node 들의 높이가 같을 수 밖에 없음을 서술 하고 있다.

B tree 의 생김새

B+ tree에서의 노드는 두가지의 종류가 있다. key - value 를 가지는 leaf - 데이터 노드와, 그것을 참조하는 index 노드이다. 이때 참조하는 노드는 leaf 노드들의 부모 노드들이다. b tree에서 모든 leaf 노드들의 depth 는 같음을 기억하자. 그렇다면 생김새를 상상해보면 leaf 노드들은 반드시 부모를 가지기 마련이다. 

다음 그림은 B+ tree의 생김새이다. 이 부분에서 결정적으로 B- tree와 결과적으로 다르게 생겼다.   

<차수 3인 B+ tree의 그림 예제, DS 과제 PDF 에서 출췌 (미상)>

위의 그림을 보면 index 노드에서 0.65 key value가 아래의 leaf node에 똑같이 존재함을 살펴보자. 0.65, 5.91, 0.58, 1.50, 20.00 은 leaf노드에 존재한다. B+ tree는 임의의 노드가 삽입되고 그것이 자신의 (차수-1) 보다 클 때, 이때 차수order 는 자신이 가질 수 있는 child 서브트리의 갯수 즉 n -ary 에서의 n을 의미한다. 이 때, 자료 갯수 n과 혼돈하지 않게 이것을 b라고하자. 이 때, b- ary이므로 자신의 subtree를 b만큼 가지게 되고, 그러면 한 노드가 그 subtree를 구간 나누는key를 b-1개 를 가질 수 있다. 즉, 임의의 노드가 들어왔는데 b와 같게 된다면 우리는 이것을 key 들 중 중간값 노드를 기준으로 split 해줘서 어떻게든 b 미만으로 만들어 줘야한다.

이 때, 처음으로 leaf 노드가 생기게되는데, B+ tree에서는 모든 노드를 leaf노드로 만들고 split 하게 만드는 key를 복사해서 index 노드로 만들어준다 !. 그렇지만 B- tree는 index node의 개념이 없고 split 하게 만드는 key 노드를 그들의 부모로 만들어주고 leaf 노드에서 삭제해준다.

위 그림에서 0.58, 0.65, 1.50, 5.91, 20.00 리프 노드를 삭제한 것을 상상해보면 그것이 B- tree가 될것이다. 이 때, 그 양상은 위와 달라질 것이지만 (당연히 차수가 3이고 노드들이 줄어들었으므로.... 노드 수가 많지 않으니 한번 그려보면 알 수 있을 것이다. )