티스토리 뷰
2차원평면에서 원의 방정식 응용 문제
컬링 게임을 하는데 컬링이 y=0인 지점부터 차곡차곡 쌓인다.
컬링은 x가 주어졌을때 (x, 10^100) 인 지점부터 y=0인 지점으로 가며 경로상에 동일한 컬링이 있을때 그곳에 부딪히고 멈춘다.
입력이 주어진것부터 컬링을 하는것이며,
인풋이 아래와 같을때 그림은 대충 저렇다.
6 2
5 5 6 8 3 12
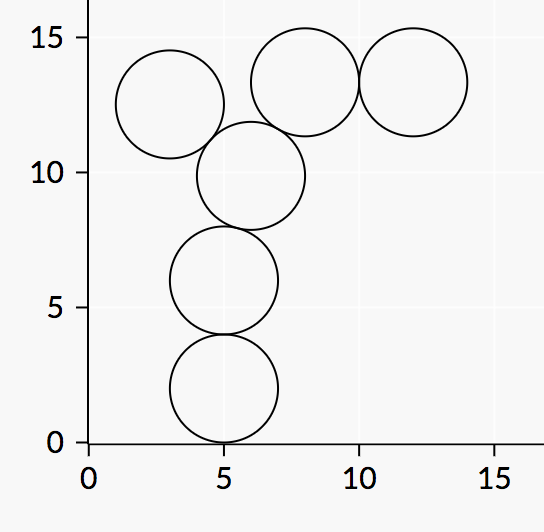
그런데 쌓이는 상태를 어떻게 저장해줘야 새로운 컬링을 그곳에 부딪힌다는 생각을 할 수 있기 때문에,
나는 이 곳에서 막혔었다.
하지만 생각해보면 결국은 이미 사용한 컬링들은 (x,y) 를 저장하고 다음 새 컬링이 올때 그것을 참조하면된다.
그렇담 y는 어떻게 결정되는가?
두 원이 접하기 위해선 다음과같은 방정식을 만족해야한다.
두 원의 반지름의 합 = 두 원의 원점 사이의 거리
따라서 x1, y1을 기존에 있던 원, x2, y2을 새로운 원이라하자. 이때 x1, y1, x2는 알고있다. 따라서
y2를 기준으로 식을 이항시킬것이다.
2 * r = sqrt( (x1-x2)^2 + (y1- y2)^2) 이며
4r^2 = (x1-x2)^2 + (y1-y2)^2
4r^2-(x1-x2)^2 = (y1-y2)^2
y2 = y1+-root( 4r^2 - (x1-x2)^2)
이다.
이때 y2는 y1보다 무조건 커야하므로 ( 왜냐하면 컬링은 항상 쌓이므로 기존의 컬링 좌표보다 높아야한다.)
y2= y1 +root( 4r^2 - (x1-x2)^2 ) 이다.
따라서 우리는 새로운 원의 y2를 구할수 있었다.
그뒤 컬링의 물리적인 이유이때문에 기존의 원 중에서 만났을 때 새로운 원의 원점이 가장 높으곳에 있어야 하기때문에 모든 기존의 원에 대해 y2를 연산하고 max만을 저장해준다.
소스보기
https://github.com/ingyeoking13/algorithm/blob/master/cf/math/908C.c
'알고리즘 문제 > math' 카테고리의 다른 글
| 삼각형의 면적 구하기, 백준 2166 다각형의 면적 (0) | 2019.03.20 |
|---|---|
| 백준 1081 합 (0) | 2019.03.09 |
| codeforces 1060C Maximum Subrectangle (0) | 2018.12.13 |
| 900B Position in Fraction (0) | 2017.12.15 |
| 878A : Short Program (0) | 2017.10.27 |
- Total
- Today
- Yesterday
- rosen
- grafana cloud
- 엄청난 인내심과 시뮬레이션을 위한 아레나 툴
- 대규모 시스템 설계 기초
- 데이터 중심 애플리케이션 설계
- 자바스크립트
- Arena
- 명제논리
- 그라파나
- Discrete Mathematics
- 아레나시뮬레이션
- 가상 면접 사례로 배우는 대규모 시스템 설계 기초
- flutter
- Propositional and Predicate Logic
- 아레나 시뮬레이션
- 이산 수학
- Grafana
- beginning javascript
- 아레나
- 로젠
- 이산수학
- paul wilton
- 백준
- 시뮬레이션
- javascript
- 자바스크립트 예제
- 항해99
- arena simulation
- 최단경로 알고리즘
- Simulation
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
