티스토리 뷰
url http://www.kocw.net/home/search/kemView.do?kemId=1064626 https://www.db-book.com/db7/slides-dir/index.html
관계 해석과 관계 대수
관계 해석(relational calculus)는 원하는 데이터만 명시하고 어떻게 질의할 것인지는 명시하지 않는 선언전인 언어. what I want. 고차원적이다.
관계 대수(relational algebra)는 어떻게 질의를 수행할 것인가를 명시하는 절차적인 언어이다. How I should do to get a thing. 저차원 적이다. 또한, 관계대수는 상용의 관계 DBMS들에서 널리 사용되는 SQL의 이론적인 기초이며, SQL을 구현하고 최적화하기 위해 DBMS의 내부 언어로서도 사용된다.
SQL
상용의 관계 DBMS들의 사실상의 표준 질의어인 SQL을 이해하고 사용할 수 있는 능력은 매우 중요하다. 사용자는 SQL을 사용하여 관계 데이터베이스에 릴레이션을 정의하고, 관계 데이터베이스에서 정보를 검색하고, 갱신하며, 여러가지 무결성 제약조건들을 명시할 수 있음.
관계 대수
1 기존의 릴레이션들로부터 새로운 릴레이션을 생성한다.
2 릴레이션이나 관계 대수식에 연산자들을 적용하여 보다 복잡한 관계 대수식을 점차적으로 만들수 있다. 마치, 수 체계에서 덧셈, 뺄셈 등의 사칙연산 또는 미적분을 수행하더라도, 그 결과에서 또한 사칙연산을 수행할 수 있듯이, 관계 대수 체계에서 점진적으로 연산이 가능하다.
3 기본적인 연산자들의 집합으로 이루어져있다.
4 산술 연산자와 유사하게 단일 릴레이션이나 두 개의 릴레이션을 입력으로 받아 하나의 결과 릴레이션을 생성한다.
5 결과 릴레이션은 또 다른 관계 연산자의 입력으로 사용 될 수 있다.
관계 대수의 기본적인 연산자
관계대수의 기본적인 연산자는 Selection, Projection, Union, Difference, Cartesian Product가 있다. 추가적으로, 편의상 사용하는 연산자는 다음과 같다. Intersection, Theta Join, Equijoin, Natural Join, Semijoin, Division이 있다. 이 연산자들은 기본적인 연산자로 부터 유도가능하다.

Cartesian Product, Division 은 강력하면서도, 연산능력이 필요하다. 최적화와 관련된 이슈들이 발생할 수도 있다. (호오..재밌겠네요?)
Selection
한 릴레이션에서 selection condition을 만족하는 tuples의 부분 집합을 return 함. 이 때, selection condition을 predicate라고도 표현한다. 단항 연산자로 동작한다.

Projection
한 릴레이션에서 특정 어트리뷰트만 포함한 릴레이션을 반환한다. 이 때, 중복된 row는 결과에서 제거되며, 결과적으로 set이 된다. 이는 Relation의 조건인, 모든 원소들은 고유하다는 조건을 만족한다. 중복 제거하기 위한 연산은, 연산량의 부하가 있다. 내가생각할땐 N^N일 듯 한데... SQL에서 Projection 수행시 해당 결과물을 중복제거하느냐 하지않느냐를 반환하는 옵션을 별도로 제공한다. 결과를 중복하지 않는 경우 엄밀히 말할 경우, 각 원소가 고유하지 않으므로 Relation이라고 표현하기는 어렵다.

Union
Union은 두 릴레이션을 합하는 것이다. 임의의 두 집합을 Union 하기 위한 조건은, compatible를 만족해야한다. 두 릴레이션의 attribute 수가 같아야하고, attribute의 순서대로의 도메인이 같아야한다. 이 경우에도, 중복된 것이 제거되므로, 릴레이션의 조건을 만족한다.

Intersection
Intersection은 compatible을 만족해야하며, 두 릴레이션에서 모두 존재하는 릴레이션을 반환한다.

Set difference도 비슷하여, 따로 설명하지 않고 넘어가자.
Cartesian Product
카테시안 프로덕트는 두 릴레이션간 모든 조합가능한 연산 결과가 나온다. A, B 테이블이 존재하고, 각 row가 X,Y. 각 attribute가 N, M이라 하자. 카테시안 결과의 Row는 X*Y 이며, attribute는 N+M이다. 카테시안 프로덕트의 결과물은 결과물로서의 의미는 크게 없다. 다만, 모든 조합의 경우의 수에서, Join 연산의 결과와 같이, 개발자/사용자에게 의미있는 릴레이션을 도출해낼 때 선행되어야 하는 연산이다.

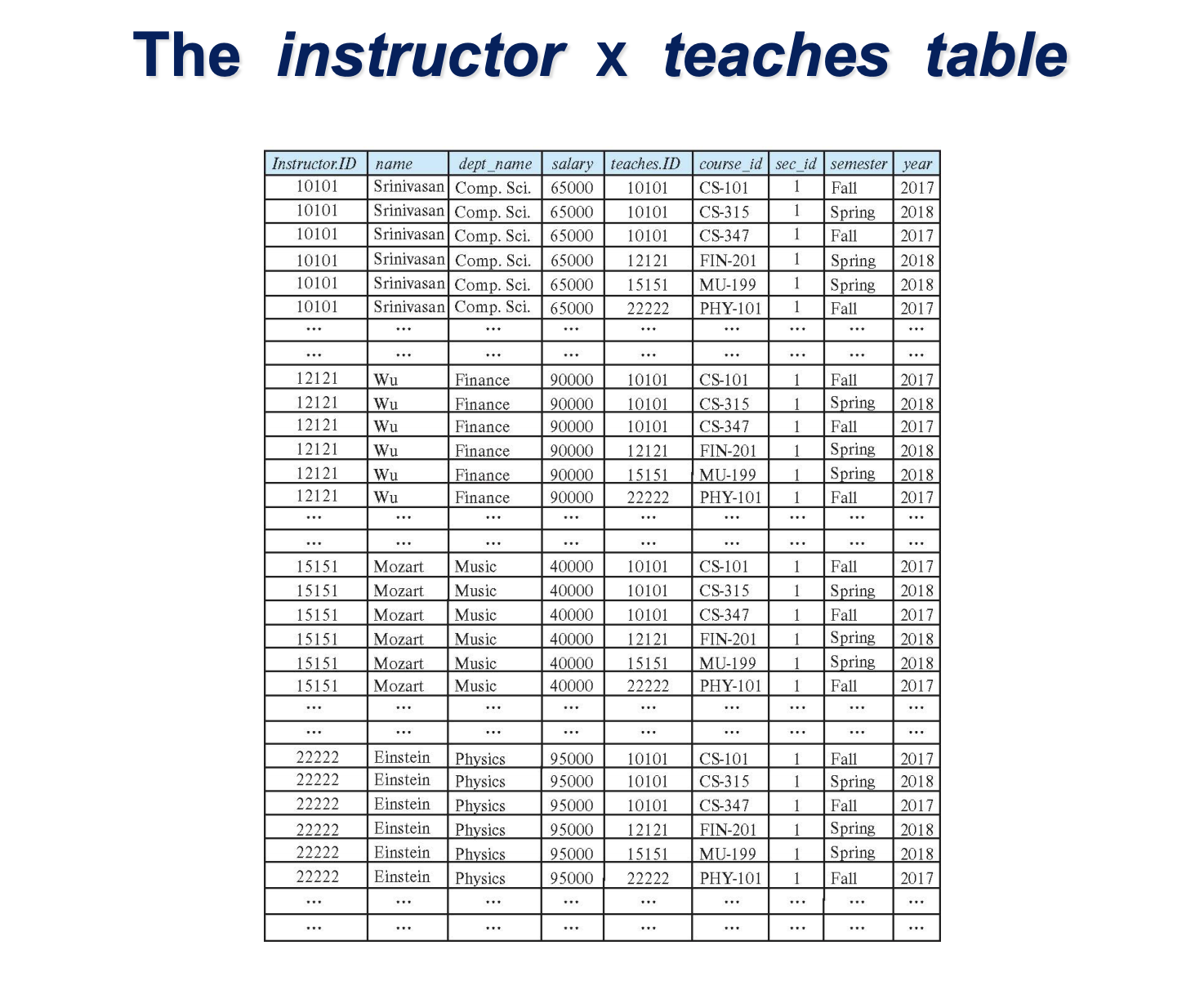
관계 대수의 완전성
Selection, Projection, Union, Difference, Cartesian Product는 관계 대수의 필수적인 연산자이다. 다른 관계 연산자들은 필수 연산자들의 조합하여 표현 가능하다. 임의의 질의어가 적어도 필수적인 관계 대수 연산자들만큼의 표현력을 갖고 있으면 관계적으로 완전하다고 한다. relationally complete.
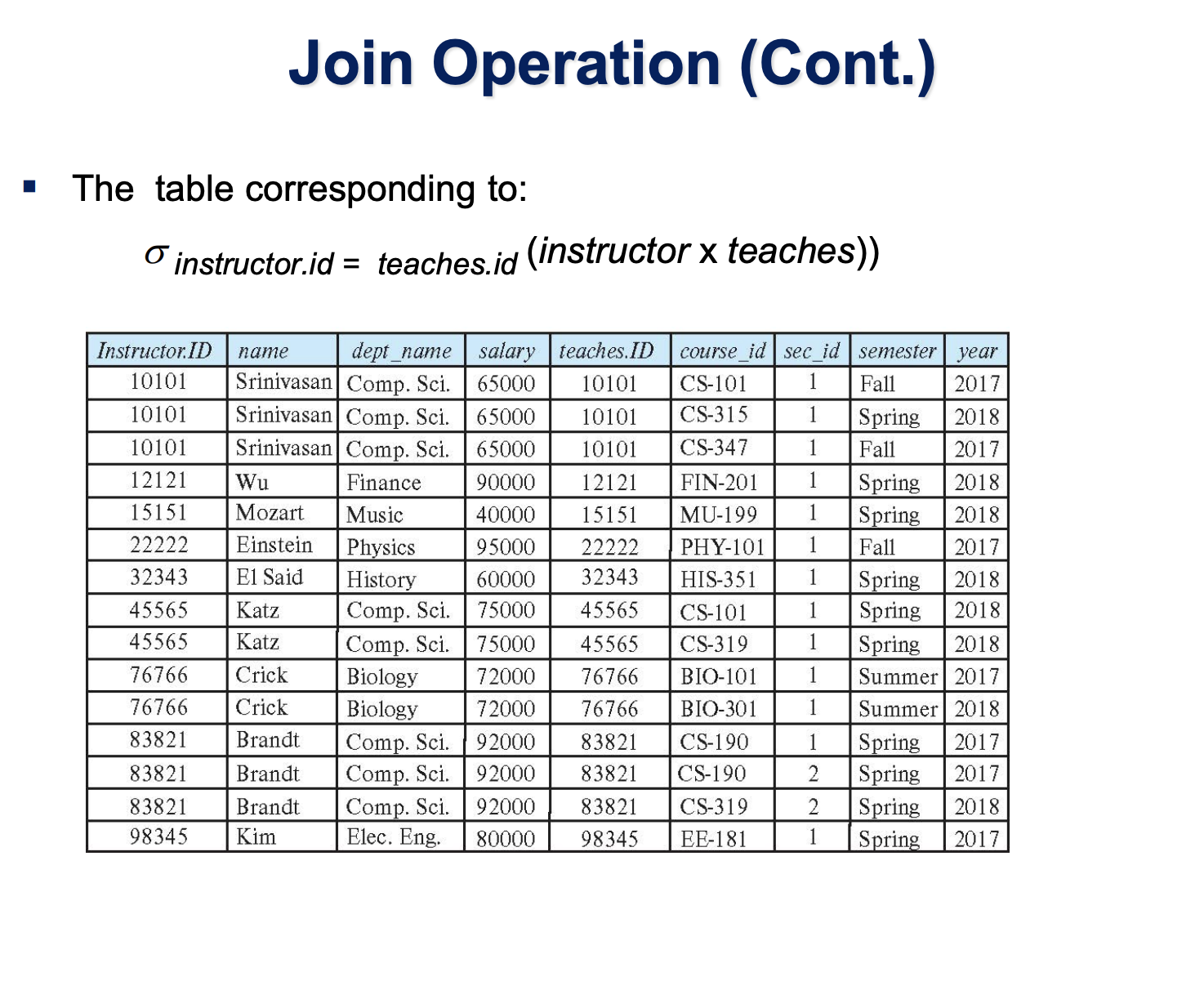
Join
두 개의 릴레이션으로부터 연관된 tuple들을 결합하는 연산자이다. Join은 cartesian product를 동반하며, Join에는 Theta Join, equijoin, natural join, outer join, semijoin등이 있다. Theta Join은 select 기호가 theta 임에 유래한 것으로 보인다. 두 릴레이션을 Cartesian Product를 수행한 결과 릴레이션에서 select를 수행한 것이 Theta Join이다. 이 때, select 조건문에 = 이 들어있으면 Equijoin이라고 한다. 이 때, 두 릴레이션에서 동일한 attribute가 있는 경우 단 하나의 attribute column만 남기고 제외된다. ( 이 경우에도, row의 cardinality 는 X*Y 임을 기억하라. ) 이를 보고 natural join이라고 하는 것이다. 즉, 일반적으로 사용하는 join은 natural join이다. outer join, semijoin은 natural join에서 특정한 옵션이 들어간 별도의 Join이다.
Join의 사용 이유는, 두 릴레이션에서 비교되는 attribute가 대소비교나 동등비교가 의미 있는 비교가능한 값들을 내포하고 있으므로 사용되는 것이다. Join을 사용 시, 의미적으로 이를 파악하여야한다.



Division
두 릴레이션간 수행될 수 있는 연산자이다. 두 릴레이션 A,B가 있을 때, B 릴레이션 attribute가 모두 A 테이블에 존재하고 있어야한다. 결과값은 B column을 제외하며, B 튜플을 소유하고 있는 릴레이션 A에 존재하는 튜플을 반환한다. 아래는 인강 프레젠테이션에서 설명하고 있는 Division 연산 이다.

*Join의 연산시 생각해볼점
Join은 많은 연산량을 필요로한다. 특히 여러 릴레이션, 2개 이상,을 수행할 때 -10개 릴레이션에 대한 cartesian product라고 생각해보자- 주 기억장치 memory로 불가능하고, disk를 이용해야한다. 이 때, disk 저장장치의 I/O를 수행해야하므로 overhead가 크다고 할 수 있다.
관계 대수의 한계
관계 대수에서는 산술 연산(+,-)을 할 수 없다. 또한, 집단 함수를 지원하지 않는다. 집단 함수란 aggregate function, 복합적인 함수의 역할이다. 예로, 산술 평균 등의 기본 지원은 하지 않는다. 또한 정렬 기능을 지원하지 않는다. 그리고 데이터 베이스를 수정하는 연산은 없다. 프로젝션 연산의 결과에서 중복된 투플을 나타내는 것이 필요할 때가 있는데 이를 명시하지 못한다.
이러한 한계점을 극복하기 위해, 확장된 관계대수에서, 집단 함수를 지원하게 되었다. 평균을 구하는 AVG, 그룹화를 하는 GROUPBY 등이 있다. 또한 외부조인 left outer join, right outer join, full outer join 등을 지원한다.
Outer Join
Outer Join 이란 두 릴레이션을 join시 포함되지 않을 튜플들도 포함시키는 것이다. 만약 right outer join인 경우, from left join right 를 수행한 후, 탈락한 right 릴레이션 투플들을 해당 릴레이션에 더한다. 이 때, left 릴레이션의 attribute는 null값을 채운다.

full outer join은 양 쪽에서 누락된 것들을 모두 더한 것이다. 혹여나, full outer join과 cartesian product와는 같다는 착각을 피하라. full outer join은, natural join이므로 적어도 =을 만족해야하므로, cartesian product와는 cardinality가 훨씬 작다.
'데이터베이스' 카테고리의 다른 글
| 인덱스 (0) | 2022.01.18 |
|---|---|
| 트랜잭션과 ACID 성질 (0) | 2022.01.16 |
- Total
- Today
- Yesterday
- Propositional and Predicate Logic
- 자바스크립트
- 로젠
- 가상 면접 사례로 배우는 대규모 시스템 설계 기초
- 아레나시뮬레이션
- arena simulation
- 그라파나
- 대규모 시스템 설계 기초
- grafana cloud
- flutter
- 최단경로 알고리즘
- 데이터 중심 애플리케이션 설계
- javascript
- paul wilton
- 시뮬레이션
- 조합 코딩
- 명제논리
- 이산수학
- beginning javascript
- Arena
- 아레나 시뮬레이션
- 이산 수학
- 엄청난 인내심과 시뮬레이션을 위한 아레나 툴
- 자바스크립트 예제
- Trie
- 백준
- Simulation
- 아레나
- rosen
- Discrete Mathematics
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 |
